Fiche proposée par Jean-Marie Lachambre, professeur au lycée Carnot de Dijon
Mesure de la masse volumique
Réflexion préalable : les limites de la méthode par les volumes
Pour déterminer expérimentalement la masse volumique d’un objet, on mesure sa masse et, pour déterminer son volume, on peut remplir d’eau une éprouvette d’un volume V1 puis après avoir immergé la roche dans d’eau, on mesure le volume V2.
Le volume de l’objet est déterminé par la différence (DV) des deux volumes d’eau (DV= V2-V1), ce qui correspond au volume d’eau déplacée par l’objet immergé.
Cette méthode n’est vraiment pas précise : pour immerger des échantillons de roches, il faut utiliser une éprouvette d’au moins 250mL. Or, le volume est mesuré avec une précision au mieux de 5 mL. L’éprouvette (et encore moins un bécher) n’est pas un instrument adapté si on souhaite une mesure précise de volume et donc de masse volumique ce qui est le cas pour nos échantillons de gabbros, de métagabbros et d’éclogites.
Rappels sur la poussée d’Archimède et la masse volumique
Tout corps plongé dans un fluide reçoit, de la part du fluide, une poussée verticale orientée vers le haut (la poussée d’Archimède, nommée ici PA) égale au poids du volume d’eau déplacé, soit : PA= m eau déplacé g
La masse volumique s’exprime par : reau = m eau déplacée/Veau déplacée soit : m eau déplacée =reau Veau déplacée
Principe de la méthode par les masses
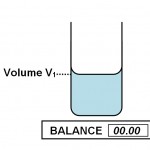 |
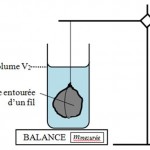 |
| 1. Placer un bécher rempli d’eau et tarer la balance. | 2. Immerger une roche dans ce bécher en veillant à ce qu’elle ne touche
ni les bords ni le fond du bécher. Lire la masse m indiquée. |
Que représente la masse m mesurée par la balance ?
L’immersion de la roche (maintenue en suspension) a donné naissance à une poussée d’Archimède orientée vers le haut ainsi qu’à une réaction en sens inverse sur la balance (principe de l’action et de la réaction).
La poussée d’Archimède (PA) est égale au poids P mesuré sur la balance (PA = P = mmesurée g).
La poussée d’Archimède (PA= m eau déplacée g) peut s’exprimer aussi en fonction du volume et de la masse volumique de l’eau (reau) : PA= reau Veau déplacée g
Au final, nous avons PA = mmesurée g = reau Veau déplacée g
Si on travaille avec les masses on a donc l’égalité mmesurée = reau Veau déplacée
Le volume de la roche est ainsi connu : V roche = Veau déplacée = mmesurée /reau
La précision est ainsi nettement augmentée puisque la masse est mesurée à 0,1g près.
Protocole « élève » de la méthode par les masses
- Mesurer d’abord la masse de l’échantillon de roche mroche (en g).
- Nouer un fil autour de la roche de façon à pouvoir tenir l’échantillon suspendu.
- Remplir au 2/3 un bécher d’eau, placer-le sur la balance. Tarer la balance.
- Immerger l’échantillon en veillant à ce qu’il ne touche ni les bords ni le fond du bécher.
- Relever la valeur m lue sur la balance qui correspond à la masse du volume d’eau déplacé.
- Sachant que la masse volumique r de l’eau est égale à : reau = m/V=1 g.cm-3, calculer le volume V (en cm3) correspondant à cette masse (m) d’eau. (en fait dans le cas présent, la valeur en g de la masse correspond à la valeur en cm3 (= mL) puisqu’il s’agit d’eau.
Ce volume correspond au volume de l’échantillon de roche (Vroche).
- Calculer la masse volumique de la roche (rroche) avec le rapport mroche / Vroche (exprimée en g.cm-3)
Remarques
– d’un point de vue scientifique, cette méthode permet à l’élève de réinvestir les notions de poussée d’Archimède et de masse volumique vues en sciences physiques.
– d’un point de vue pratique, le travail peut se faire avec de petits échantillons (50g par exemple) tout en ayant une précision très satisfaisante. Cela permet de travailler sur les petites différences (mais très significatives) de densité entre gabbro et métagabbro, métagabbro à glaucophane et éclogite,…
Astuces :
– pour maintenir l’échantillon immobile, il est nécessaire d’utiliser une potence.
– pratiquant cette technique avec mes élèves depuis plusieurs années, j’ai constaté que nouer un fil autour d’un échantillon de roche n’est pas simple. Maintenant je place d’abord un élastique fin autour de l’échantillon puis je passe un fil (de coton par exemple) sous l’élastique.
Exemples de valeurs obtenues avec mes élèves :
| Roches |
Masse (mroche) en g |
Volume (Vroche) en cm3 |
Masse volumique (rroche) en g.cm-3 |
| Granite |
67,3 |
25,9 |
2,60 |
| Basalte |
63,18 |
23,4 |
2,70 |
| Gabbro |
63,36 |
22,8 |
2,78 |
| Métagabbro à hornblende(Chenaillet) |
78,88 |
28,2 |
2,80 |
| Métagabbro à glaucophane (Queyras) |
67,68 |
22,5 |
3,01 |
| Eclogite |
94,58 |
29,8 |
3,17 |
| Péridotite |
72,19 |
22,4 |
3,22 |